【超入門IT講座】現代社会に必須!データベースのキホン①
どうもみなさんこんにちは、IT修行中のななこです!ここでは、IT超初心者の私が知りたい!と思ったことにスポットを当て、「なるほど!」と感じたことをご紹介します!今回はITエンジニアになるなら知っておくべき「データベース」の基本について学んだことをお話しますね✨1. データベースとは?データベースは、アプリケーションのデータを保存・蓄積するための手段です!大量のデータを蓄積しておいて、そこから必要な
Workteria(ワークテリア)では難易度の高いものから低いものまで、スキルや経験に合わせた案件を多数揃えています。会員登録は無料ですので、ぜひ会員登録してご希望の案件を探してみてください!
フリーランス/正社員のエンジニアとして活躍するには、ご自身のスキルや経験に合わせた仕事を選ぶことが大切です。ご希望の案件がみつからない場合はお気軽にお問い合わせください!ユーザ満足度の高いキャリアコンサルタントが在籍していますので、希望条件や悩み事などなんでもご相談ください。ご希望にピッタリの案件をご紹介させていただきます。
基数とは、数値を扱う際に「基となる数字の個数(ひとつの桁を表すのに何個の数字が扱われるか)」のことを指します。
この記事を読むことで、
・進数の変換方法(重みを使った方法・割り算と掛け算での方法)
・桁が持つ重みについて以上のことが分かります。
また、基数・進数・桁の重みについてより詳しく知りたい方は、
をご一読ください。基数についてより知ることができます!

基数変換とは、2進数を10進数に変換したり、16進数を10進数に変換したり、現状において必要な進数に変換する方法です。
どうして置き換える必要が出てくるのでしょうか?
一般的に海外の方と会話をする際、その方が分かる言語(例えば、英語)で話さなければ、会話は成立しません。そのため、英語を習得したり、翻訳機を使ったりして、なんとか話を伝える必要があります。
コンピュータも同じで、コンピュータで扱う数値は、2進数で表される「0・1」のみです。
そのため、私たちは2進数で情報のやり取りをする必要があるのです。
しかし、私たちが一般的に使用する数値は10進数です。
そのため、コンピュータとのやりとりでは、2進数を10進数に、または10進数を2進数に変換しないと、数値が分かりません。
そこで、基数変換が必要になるのです。
基数変換の前に、重要な各基数の桁が持つ「重み」について解説します。
まず、2進数の桁上がりを見てみましょう。
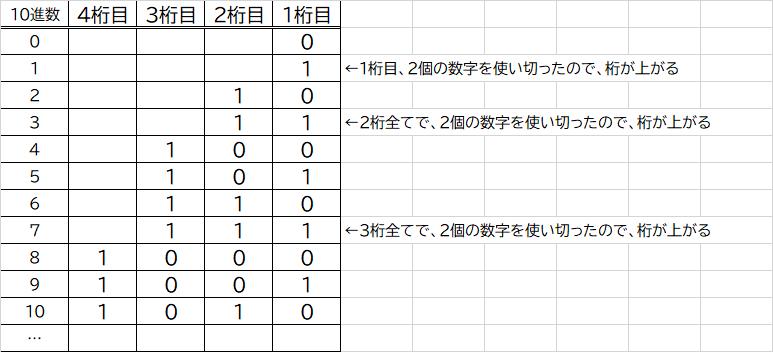
1桁目で2個(0・1)の数字を全て使い切ると、1の次に当たる数字が2進数には存在しないため、桁上がりをし「10」となります。
桁上がりをすると、また1桁目から数字が増えていきます。
また、2桁目でも1番大きな数字の1までを使い切ったので、桁上がりをし「100」となります。
この桁上がりする際、ある規則的な値が出てくるのですが分かるでしょうか?
答えは、「倍々となって増えていく」です。
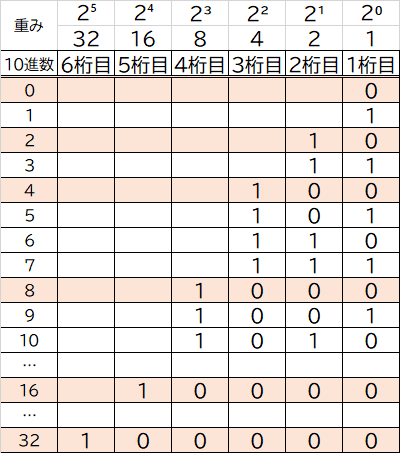
1桁目は2の0乗(2⁰)
2桁目は2の1乗(2¹)
3桁目は2の2乗(2²)
4桁目は2の3乗(2³)
5桁目は2の4乗(2⁴)
6桁目は2の5乗(2⁵)というように、桁が上がるごとに
1 → 2 → 4 → 8 → 16 → 32と倍々になっているのです。
この倍となっていく数字が、2進数が持つ各桁の「重み」といいます。
つまり、桁ごとに「2の(桁数‐1)乗」を行った数値で重みがわかるのです。
10進数の各桁の重みも見てみましょう。
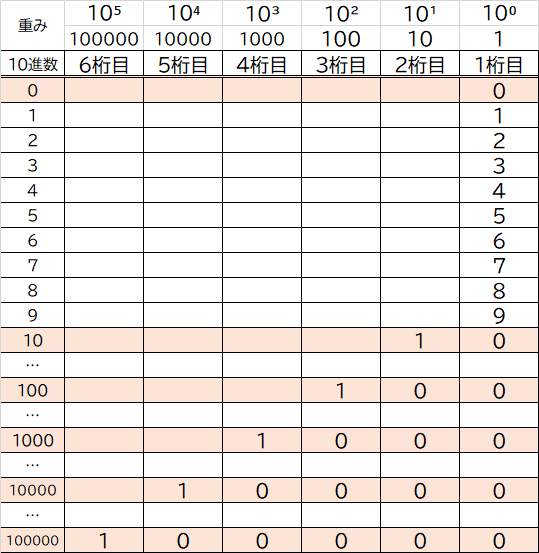
1 → 10 → 100 → 1000 → 10000 → 100000
桁が上がるごとに倍々になっていっているのが分かります。
また、桁ごとの重みは「10の(桁-1)乗」を行った数値になっています。
※1以下の数値については、倍々で小さくなっていきます。
2進数の場合、1/2→1/4→1/8…と倍々で小さくなっていきます。

重みについて理解できたところで、n進数から10進数への基数変換をしてみましょう。
n進数のnには、変換したい元の基数が入ります。
nには、2進数や8進数の2や8が入るということです。
n進数を10進数へ変換するには、
各桁の重みを掛け、結果を足すことで10進数への変換ができます。2進数「1011.101」を10進数に変換してみます。
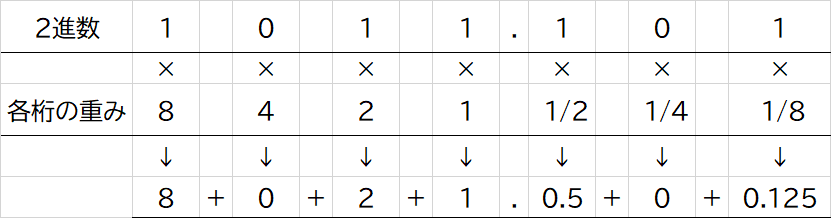
2進数「1011.101」は各桁の重みを掛けた結果
8 + 0 + 2 + 1 + 0.5 + 0 + 0.125
=11.62510進数「11.625」となり、
これで、2進数から10進数への基数変換ができました。
8進数・16進数なども、2進数と同じ方法で10進数への基数変換が可能です。
<8進数>
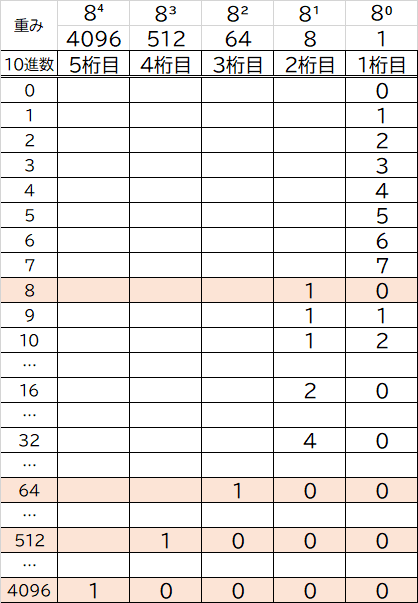
8進数「1725.63」を重みを使って10進数へ変換すると
(512×1)+(64×7)+(8×2)+(1×5)+(0.125×6)+(0.015625×3)
=512 + 448 + 16 + 5 + 0.75 + 0.046875
=981.79687510進数「981.796875」となります。
<16進数>
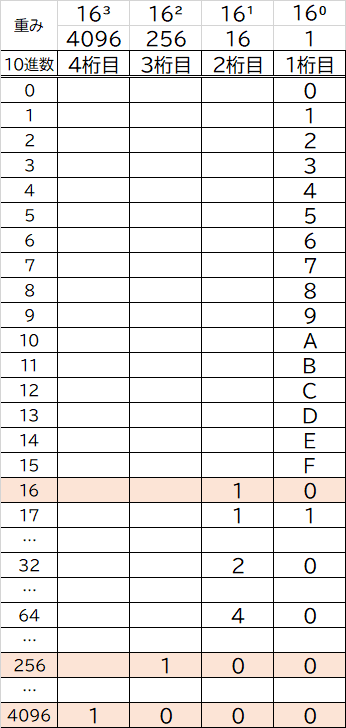
16進数「3D5.29」を重みを使って10進数へ変換すると
(256×3)+(16×13)+(1×5) + (0.0625×2)+(0.00390625×9)
=768 + 208 + 5 + 0.125 + 0.03515625
=981.1601562510進数「981.16015625」となります。
n進数を10進数へ基数変換する場合、
①各桁の重みをかける
②かけて出た結果を足す以上の2工程を経て10進数への変換をすることができます。
10進数からn進数への基数変換には2つの方法があります。
・各桁の重みを使った変換方法
・割り算と掛け算を使った変換方法基数の各桁が持つ「重み」を使って行う方法について解説します。
前の項目では、n進数から10進数への変換を、各桁の重みを「掛け算」して行いました。
逆の10進数からn進数への変換は、各桁の重みを順に「割り算」します。
先ほど2進数から10進数への変換を行った際に出た10進数「11.625」を2進数に変換してみます。
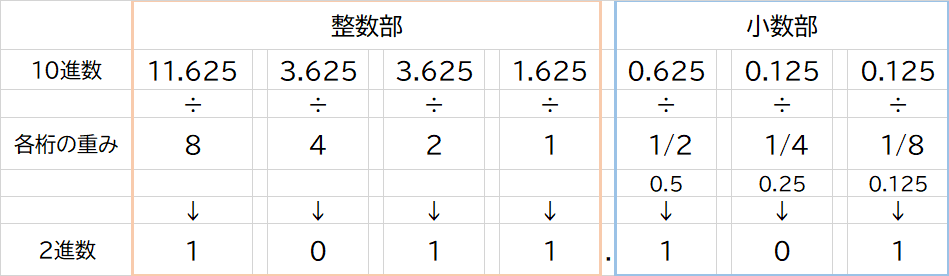
整数部
① 11 ÷ 8 = 1 … 3
② 3 ÷ 4 = 0 … 3
③ 3 ÷ 2 = 1 … 1
④ 1 ÷ 1 = 1 … 0
小数部
⑤ 0.625 ÷ 0.5 = 1 … 0.125
⑥ 0.125 ÷ 0.25 = 0 … 0.125
⑦ 0.125 ÷ 0.125 = 1 … 02進数「1011.101」
整数部は整数部分各桁の重みを使って割り算を、
小数部は小数部分各桁の重みを使って割り算をそれぞれ順に計算していきます。
2進数部分には、商を入れます。
これで、10進数から2進数への各桁の重みを使って変換が出来ました。
変換したい基数を使って、整数部は割り算・小数部は掛け算をして行う方法について解説します。
ここでも、先ほどと同じ数値の10進数「11.625」を2進数に変換してみます。
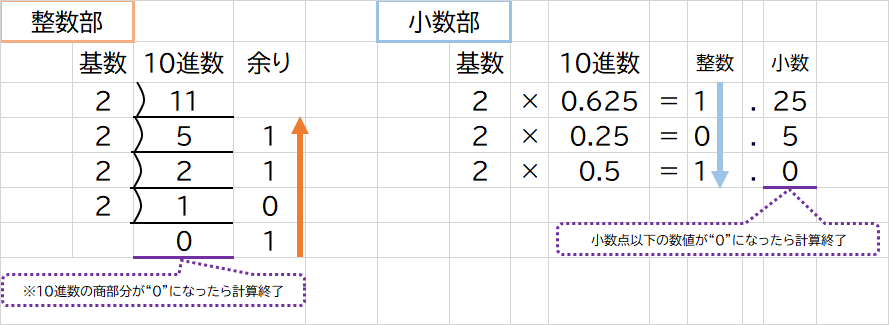
整数部
① 11 ÷ 2 = 5 … 1
② 5 ÷ 2 = 2 … 1
③ 2 ÷ 2 = 1 … 0
④ 1 ÷ 2 = 0 … 1
小数部
⑤ 0.625 × 2 = 1.25
⑥ 0.25 × 2 = 0.5
⑦ 0.5 × 2 = 1.02進数「1011.101」
整数部は余りを④→③→②→①と降順に
小数部は整数になった部分を⑤→⑥→⑦と昇順にそれぞれ記載します。
これで、10進数から2進数へ割り算と掛け算を使って変換することが出来ました。

8進数と16進数は、2進数との変換がしやすい進数です。
8進数は2³(2の3乗)
16進数は2⁴(2の4乗)となっています。
8進数は3桁で、16進数は4桁でそれぞれを区切って変換をしていきます。
2進数「1011.101」を8進数に変換してみましょう。

①3桁ごとに区切る(3桁に満たない部分には“0”を補う)
②区切った単位ごと、それぞれを8進数に変換する
③8進数に変換した数値を並べる2進数、3桁までで表せる最大値は、
2進数「111」=10進数「7」
となります。
8進数は0~7の数値を扱うので、2進数を3桁に分けることで、8進数となるのです。
反対に、8進数を2進数に変換する場合は
各桁を2進数の3桁に分けることで変換ができます。

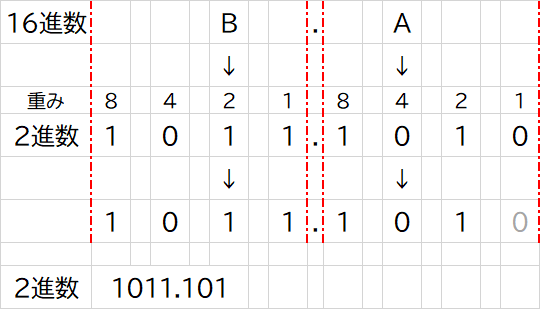
2進数「1011.101」を16進数に変換してみましょう。

①4桁ごとに区切る(4桁に満たない部分には“0”を補う)
②区切った単位ごと、それぞれを16進数に変換する
③16進数に変換した数値を並べる進数、4桁までで表せる最大値は、
2進数「1111」=10進数「15」
となります。
16進数は0~9と A ~ F の数値を扱うので、2進数を4桁に分けることで、16進数となるのです。
反対に、16進数を2進数に変換する場合は
各桁を2進数の4桁に分けることで変換ができます。
基数変換について、分かったでしょうか?
変換方法にはいくつかあるので、自身のやりやすい方法を覚えておくと良いでしょう。
そのような方はぜひ、Workteriaサイトをご利用ください!
定期的にご本人に合う高額案件を紹介
リモートワークなど自由な働き方ができる案件多数
専属エージェントが契約や請求をトータルサポート