【超入門IT講座】現代社会に必須!データベースのキホン①
どうもみなさんこんにちは、IT修行中のななこです!ここでは、IT超初心者の私が知りたい!と思ったことにスポットを当て、「なるほど!」と感じたことをご紹介します!今回はITエンジニアになるなら知っておくべき「データベース」の基本について学んだことをお話しますね✨1. データベースとは?データベースは、アプリケーションのデータを保存・蓄積するための手段です!大量のデータを蓄積しておいて、そこから必要な
Workteria(ワークテリア)では難易度の高いものから低いものまで、スキルや経験に合わせた案件を多数揃えています。会員登録は無料ですので、ぜひ会員登録してご希望の案件を探してみてください!
フリーランス/正社員のエンジニアとして活躍するには、ご自身のスキルや経験に合わせた仕事を選ぶことが大切です。ご希望の案件がみつからない場合はお気軽にお問い合わせください!ユーザ満足度の高いキャリアコンサルタントが在籍していますので、希望条件や悩み事などなんでもご相談ください。ご希望にピッタリの案件をご紹介させていただきます。
数学やIT関係の勉強をしていると、何度か出てくる「基数」という言葉があります。
IT関係のことを学んでいく上では、とても重要な基礎になります。
この記事を読むことで、
・基数とは何か
・2進数(進数)について以上のことが分かります。
ITパスポート試験や基本情報技術者試験などのIT系国家試験を学ぶ際、基数や2進数は基礎知識として必要となります。
知らない方は、ぜひ一読してみてください。

「基数」とは、数値を扱う際に「基となる数字の個数」のことです。
詳しく見てみましょう。
私たちが数をかぞえる時、基になる数字はいくつあるでしょうか?

上記の10個です。
この10個の数字を使うことで、億や兆まで、逆はマイナスや小数点以下の数値まで、全てを表すことができます。
コンピュータ上(デジタル上)では、数を扱う際、基となる数字は、
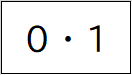
上記の2個のみです。
コンピュータ上では、この2個の数字だけで、メガやギガなどの大きなものやマイクロやナノなどの小さな数値までのすべてを表すことができるのです。
この、基となる数字の個数(ひとつの桁を表すのに何個の数字が扱われるか)のことを“基数”と呼びます。
「基数」とは、数値を数えるうえで基となる数のことを指すことがわかりました。
基数と共に覚えておく言葉として「進数」があります。
基数が10のものを「10進数」
基数が2のものを「2進数」と呼びます。
10進数で詳しく解説していきます。
10進数とは、基となる数字が10個、言い換えると
「10個の数字が使える」と言うことです。
また、「10になるごとに桁が上がる」と言うことです。
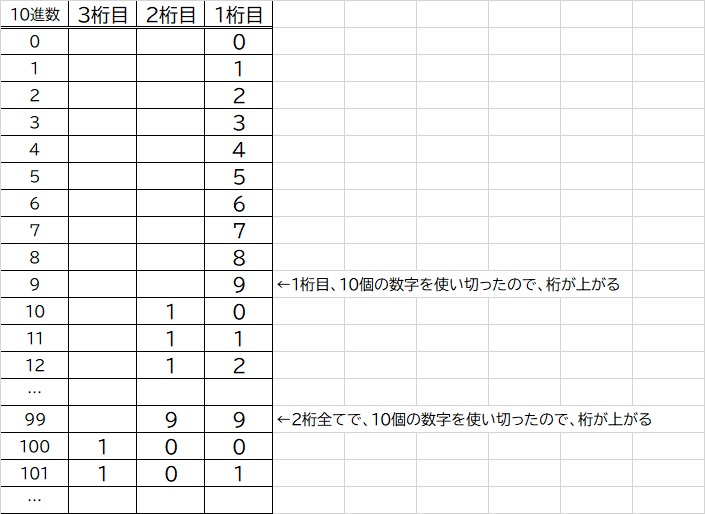
1桁目で10個(0~9)の数字を全て使い切りました。
そうすると、9の次に当たる数字が10進数には存在しないため、桁上がりをし「10」となります。
桁上がりをすると、また1桁目から数字が増えていきます。
また、2桁目でも1番大きな数字の9までを使い切ったので、桁上がりをし「100」となります。
このように、その桁で0~9までの10個の数字を使い切ると、桁が上がるものを「10進数」と呼びます。
それでは、2進数ではどうなるでしょうか?
2進数は、基となる数字が2個、言い換えると
「2個の数字が使える」「2になるごとに桁が上がる」ということです。
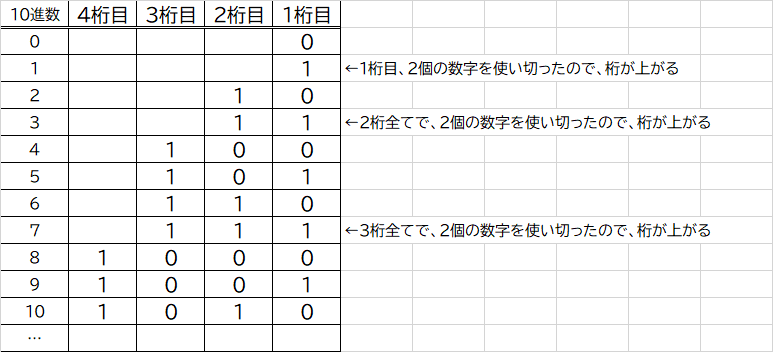
1桁目で2個(0・1)の数字を全て使い切りました。
そうすると、1の次に当たる数字が2進数には存在しないため、桁上がりをし「10」となります。
桁上がりをすると、また1桁目から数字が増えていきます。
また、2桁目でも1番大きな数字の1までを使い切ったので、桁上がりをし「100」となります。
このように、その桁で0と1の2個の数字を全て使い切ると、桁が上がるものを「2進数」と呼びます。
8進数と16進数も見てみましょう。
《8進数》
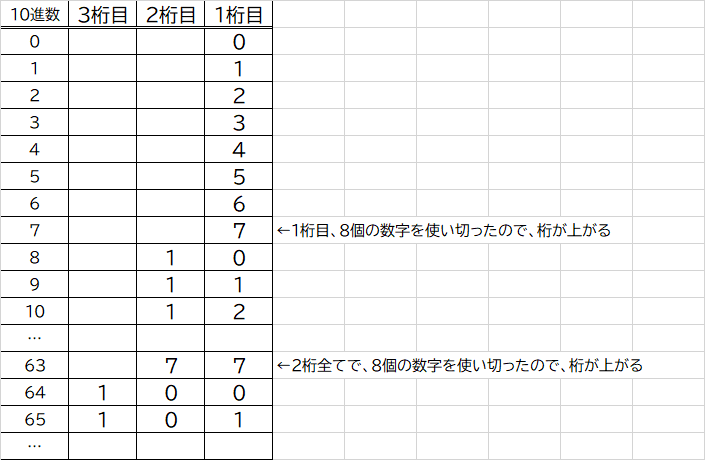
8進数は、0~7までの8個の数字をつかって数値を表します。
そのため、1桁目で8個の数字をすべて使い切り、7の次に当たる数字が8進数には存在しないため、桁上がりをし「10」となります。
《16進数》
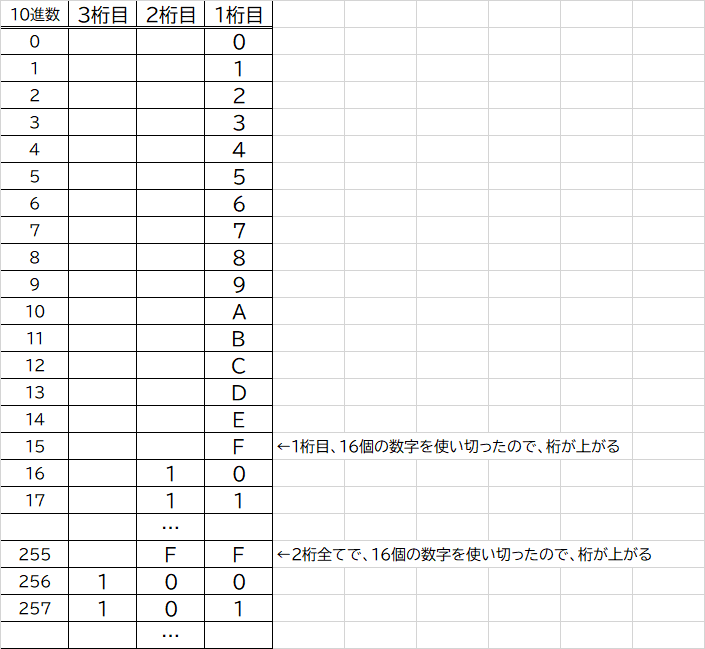
16進数は、0~9 と A~F までの16個の数字をつかって数値を表します。
そのため、1桁目で16個の数字をすべて使い切り、Fの次に当たる数字が16進数には存在しないため、桁上がりをし「10」となります。
ここまでの進数についてまとめると、
「n進数」とは n が基数であり、
n 個の数字を使い切ると桁上がりをするものということになります。

2進数表記の数値を10進数で表したい、ということがあった場合には、「基数変換」が必要になります。
2進数「1010」を10進数にする場合、桁ごとに「2の(桁数‐1)乗」を行った数値の「重み」を使うことで、基数変換ができます。
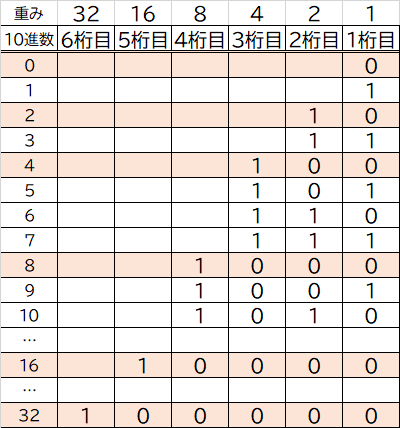
2進数の各桁に重みを掛けます。その重みのついた値全てを足し合わせると、10進数への変換ができます。
2進数「1010」は、
4桁目が1、3桁目が0、2桁目が1、1桁目が0 になっています。
以上を元に計算をしてみます。
1×2³+1×2¹
=1×(2×2×2)+1×2
=1×8+1×2
=8+2
=102進数「1010」が10進数「10」へ変換が出来ました。
このように各桁の重みを使うことで、変換ができます。
他には、割り算と掛け算を使って基数変換する方法もあります。
より詳しい基数変換について知りたい方は、
で詳しく解説しているので、ぜひ一読してみてください。
 10進数で足し算・引き算ができるように、他の基数での足し算・引き算も可能です。
10進数で足し算・引き算ができるように、他の基数での足し算・引き算も可能です。

2進数の足し算では、
・0+0=0
・1+0=1(0+1=1)
・1+1=10以上の3種類で計算ができます。
2進数では「0と1」しか表現できない基数のため、1+1は桁上がりがおきるのです。

2進数の引き算では、
・0-0=0
・1-1=0
・1-0=1
・0-1=1以上の4種類で計算ができます。
0-1=1の計算に関しては、0から1が引けないため、上の桁から“1”を借りてきます。
10進数でも、引き算元の数値が足りない場合は、上の桁から数字を借りてきますよね、それと同じです。
また、引き算に関しては、「補数」の考え方が必要になる場合もあります。
より詳しい基数の足し算・引き算・補数について知りたい方は、
2進数の足し算・引き算(加減算)の方法と正の数・負の数、補数について解説!
で詳しく解説しているので、ぜひ一読してみてください。

10進数で掛け算・割り算ができるように、他の基数での掛け算・割り算も可能です。

元の数値を左にシフトすることで、掛け算(2のn乗)ができます。
空いた桁には“0”を入れます。
2進数「1010」(10進数「10」)を左に1シフトすることで、
2進数「10100」(10進数「20」)になり2倍にできました。

元の数値を右にシフトすることで、割り算( 1/2のn乗)ができます。
“0”があふれた場合は、消します。
2進数「1010」(10進数「10」)を右に1シフトすることで、
2進数「101」(10進数「5」)になり1/2倍(半分)にできました。
上記で説明した方法は、「シフト演算」という考えを元にしています。
また、シフト演算には2つの種類があります。
「論理シフト」と「算術シフト」です。
上記で説明したものは、「論理シフト」に該当します。
「算術シフト」は、論理シフトに符号(+,-)が付いたものになります。
より詳しい基数の掛け算・割り算・シフト演算について知りたい方は、
2進数の掛け算・割り算(乗除算)の方法とシフト演算(論理シフトと算術シフト)について
で詳しく解説しているので、ぜひ一読してみてください。
2進数の数値を表す方法で、「固定小数点数」と「浮動小数点数」というものがあります。
2進数の1桁は「1ビット」、8桁で「8ビット(1バイト)」です。
この8ビットの中で、小数点を使って数値を表そうとした場合において
・ビット列のどの位置に小数点があるか、決まっている数値を表現するものを「固定小数点数」
・ビット列の小数点を移動させ、移動させた分を指数表記で数値を扱うものを「浮動小数点数」固定小数点数は、事前に小数点の位置が決められている場合にのみ用いられます。

例えば、頭から5ビット分を整数、と決めた(決まっていた)ら、「10001.011」となります。
(符号(+、-)ありの場合は、一番左のビット列が符号用になります)
浮動小数点は、小数点の位置を移動させ、移動した分を指数に表します。

小数点を移動させたことで、表現できる数値が3桁分増えました。
固定小数点では、表せる整数に限りがあります。
しかし、浮動小数点を扱うことで、表せる範囲が広がるのです。
より詳しい基数の小数点(固定小数点数・浮動小数点数)や正規化について知りたい方は、
2進数の小数点(固定小数点数・浮動小数点数)の表し方と正規化について
で詳しく解説しているので、ぜひ一読してみてください。

浮動小数点では、小数点を移動させることで、表せる数値が増えます。
そのため、小数点以下の数値が多い場合において、大変有効な表現方法です。
しかし、無限小数(割り切れない数値、例えば10÷3など)の場合においては、決められたビット数内で納めなければならないため、本来の数値とは若干違う「誤差」が出ることがあります。
四捨五入や切り捨てなどを行い、生じる誤差を「丸め誤算」
正規化で小さな値が切られてしまい、生じる誤差を「情報落ち」など、浮動小数点を使ったことで生じてしまう誤差にも種類があります。
より詳しい基数の浮動小数点と誤差について知りたい方は、
浮動小数点数の誤差について(無限小数・桁あふれ誤差・情報落ち・打切り誤差・桁落ち・丸め誤差)
で詳しく解説しているので、ぜひ一読してみてください。
基数や進数、重みについて分かったでしょうか?
2進数は、IT系の仕事や資格では必須の基本的なものになります。
ぜひ、他のページも読んでマスターしてみましょう!
そのような方はぜひ、Workteriaサイトをご利用ください!
定期的にご本人に合う高額案件を紹介
リモートワークなど自由な働き方ができる案件多数
専属エージェントが契約や請求をトータルサポート